Easy as a cake, after we learn.
Explicit 2D scalar wave equation
The scalar wave equation, a fluid medium with variable velocity, is defined by (\ref{ExpA}) Where $U$ and $V$ represents the pressure (or scalar displacement) and velocity fields and S(t) the source, and can be simplified in (\ref{ExpB}) for 2D case:
\begin{eqnarray}
\frac{\partial^2 U}{\partial t^2} \frac{1}{V^2} &=& \nabla^2 U + S(t) \label{ExpA} \\
\frac{\partial^2 U}{\partial t^2} &=& V^2 \left( \frac{\partial^2 U}{\partial x^2}+ \frac{\partial^2 U}{\partial z^2} +S(t) \right)
\label{ExpB}
\end{eqnarray}
From equation (\ref{ExpB}) we can approximate derivatives by Taylor series, manipulating we can reach centered differences in time (second order time) and centered in space N'th order; using $Dx=Dz=Ds$, remember that $j=jDs$, $k=kDs$ and $n=nDt$.
\begin{eqnarray}
U_{jk}^{n+1} &=& \left( \frac{\Delta t V_{jk} }{\Delta s} \right) ^2 \left( \sum_{a=-N}^N w_a U_{j+a k}^n + \sum_{a=-N}^N w_a U_{j k+a}^n +S_{jk}^n {\Delta s}^2 \right) + 2 U_{jk}^{n} - U_{jk}^{n-1} \\
U_{jk}^{n+1} &=& \left( \frac{\Delta t V_{jk}}{\Delta s} \right) ^2 \left[ \sum_{a=-N}^N w_a \left( U_{j+a k}^n + U_{j k+a}^n \right) \right] + S_{jk}^n {\Delta t}^2 V_{jk}^2 + 2 U_{jk}^{n} - U_{jk}^{n-1} \\
U_{jk}^{n+1} &=& \left( \frac{\Delta t V_{jk}}{\Delta s} \right) ^2 \left[ \sum_{a=-N}^N w_a \left( U_{j+a k}^n + U_{j k+a}^n \right) + S_{jk}^n {\Delta s}^2\right] + 2 U_{jk}^{n} - U_{jk}^{n-1} \label{ExpC}
\end{eqnarray}
For forth order space, we have $N=2$ and $w$ is:
$$ w = \frac{1}{12} [-1, 16, -30, 16, -1] $$
To make the approximate finite differences solution (or series) not explode and be bounded to the correct solution $ R $ must always be bounded (the stability criteria):
\[ R = \frac{\Delta t V_{max}}{\Delta s} \]
Where $V_{max}$ is the maximum velocity.
Based on work and simplified from Chen [2] the forth order schema requires :
$$ \Delta t \leq \frac{2 \Delta s}{ V_{max} \sqrt{2/12(1+16+30+16+1)}} \implies \Delta t \leq \frac{ \Delta s \sqrt{3}}{ V_{max} \sqrt{8}} = \frac{ \Delta s \sqrt{3}}{ V_{max} \sqrt{8}}$$
Must also be highlighted that the closer $\Delta t$ is to the limit above better is the solution.
Implementation:
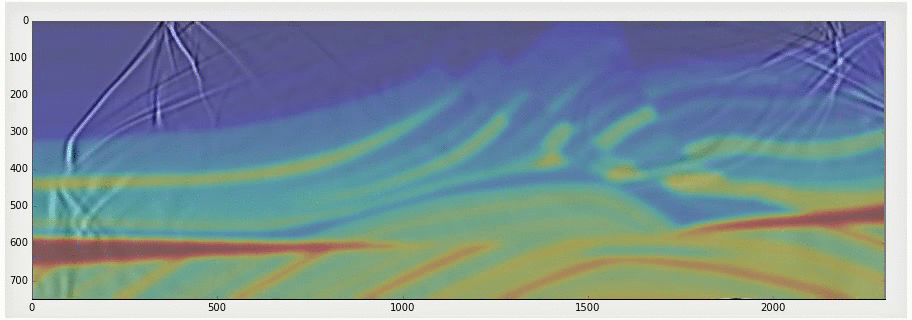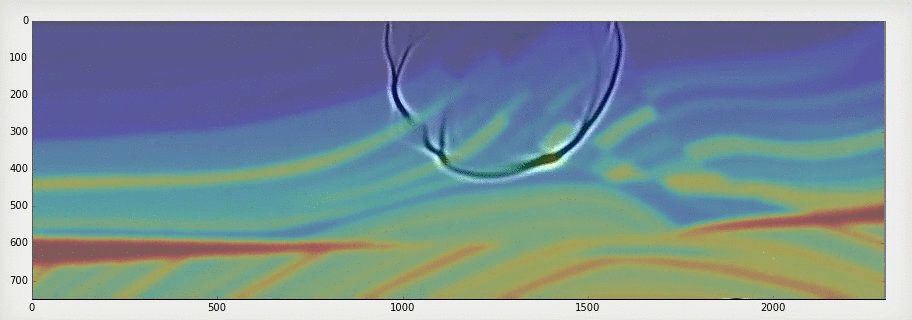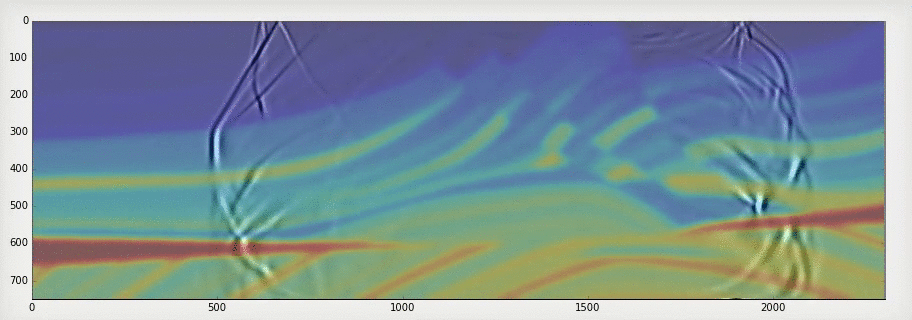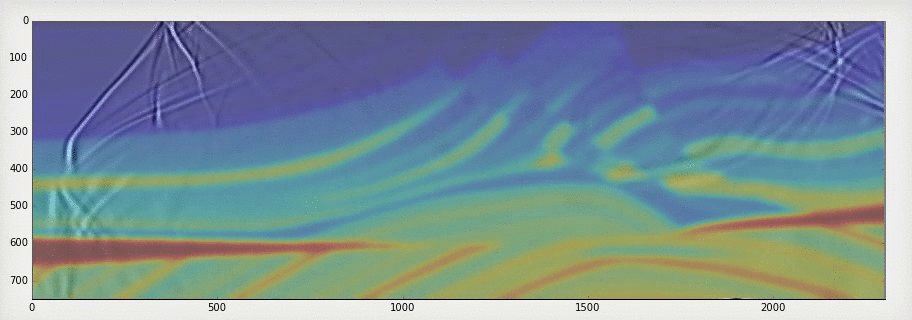
Simple example using fatiando and Marmousi velocity model.
Jupyter notebook here.
References
[1] Alford R.M., Kelly K.R., Boore D.M. (1974) Accuracy of finite-difference modeling of the acoustic wave equation Geophysics, 39 (6), P. 834-842
[2] Chen, Jing-Bo (2011) A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation Geophysics, v. 76, p. T37-T42
Explicit 2D scalar wave equation
The scalar wave equation, a fluid medium with variable velocity, is defined by (\ref{ExpA}) Where $U$ and $V$ represents the pressure (or scalar displacement) and velocity fields and S(t) the source, and can be simplified in (\ref{ExpB}) for 2D case:
\begin{eqnarray}
\frac{\partial^2 U}{\partial t^2} \frac{1}{V^2} &=& \nabla^2 U + S(t) \label{ExpA} \\
\frac{\partial^2 U}{\partial t^2} &=& V^2 \left( \frac{\partial^2 U}{\partial x^2}+ \frac{\partial^2 U}{\partial z^2} +S(t) \right)
\label{ExpB}
\end{eqnarray}
From equation (\ref{ExpB}) we can approximate derivatives by Taylor series, manipulating we can reach centered differences in time (second order time) and centered in space N'th order; using $Dx=Dz=Ds$, remember that $j=jDs$, $k=kDs$ and $n=nDt$.
\begin{eqnarray}
U_{jk}^{n+1} &=& \left( \frac{\Delta t V_{jk} }{\Delta s} \right) ^2 \left( \sum_{a=-N}^N w_a U_{j+a k}^n + \sum_{a=-N}^N w_a U_{j k+a}^n +S_{jk}^n {\Delta s}^2 \right) + 2 U_{jk}^{n} - U_{jk}^{n-1} \\
U_{jk}^{n+1} &=& \left( \frac{\Delta t V_{jk}}{\Delta s} \right) ^2 \left[ \sum_{a=-N}^N w_a \left( U_{j+a k}^n + U_{j k+a}^n \right) \right] + S_{jk}^n {\Delta t}^2 V_{jk}^2 + 2 U_{jk}^{n} - U_{jk}^{n-1} \\
U_{jk}^{n+1} &=& \left( \frac{\Delta t V_{jk}}{\Delta s} \right) ^2 \left[ \sum_{a=-N}^N w_a \left( U_{j+a k}^n + U_{j k+a}^n \right) + S_{jk}^n {\Delta s}^2\right] + 2 U_{jk}^{n} - U_{jk}^{n-1} \label{ExpC}
\end{eqnarray}
For forth order space, we have $N=2$ and $w$ is:
$$ w = \frac{1}{12} [-1, 16, -30, 16, -1] $$
To make the approximate finite differences solution (or series) not explode and be bounded to the correct solution $ R $ must always be bounded (the stability criteria):
\[ R = \frac{\Delta t V_{max}}{\Delta s} \]
Where $V_{max}$ is the maximum velocity.
Based on work and simplified from Chen [2] the forth order schema requires :
$$ \Delta t \leq \frac{2 \Delta s}{ V_{max} \sqrt{2/12(1+16+30+16+1)}} \implies \Delta t \leq \frac{ \Delta s \sqrt{3}}{ V_{max} \sqrt{8}} = \frac{ \Delta s \sqrt{3}}{ V_{max} \sqrt{8}}$$
Must also be highlighted that the closer $\Delta t$ is to the limit above better is the solution.
Implementation:
- Last line in equation (\ref{ExpC}) describes the time step forward implementation (second order in time and forth in space) for a 2D grid.
- To guarantee stability the Laplacian should not be contaminated, just multiply by R.
- Use an epsilon $\epsilon$ (like 10^-4) to make $\Delta t$ closer to its limit of convergence. Like $\Delta t = \frac{ \Delta s \sqrt{3}}{ V_{max} \sqrt{8}}*(1-\epsilon) $
Simple example using fatiando and Marmousi velocity model.
Jupyter notebook here.
References
[1] Alford R.M., Kelly K.R., Boore D.M. (1974) Accuracy of finite-difference modeling of the acoustic wave equation Geophysics, 39 (6), P. 834-842
[2] Chen, Jing-Bo (2011) A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation Geophysics, v. 76, p. T37-T42
Comments
Post a Comment